Suppose we wish to generate a sequence of 10000000 random 32-bit integers with no repeats. How can we do it?

I faced this problem recently, and considered several options before finally implementing a custom, non-repeating pseudo-random number generator which runs in O(1) time, requires just 8 bytes of storage, and has pretty good distribution. I thought I’d share the details here.

Approaches Considered

There are already several well-known pseudo-random number generators (PRNGs) such as the Mersenne Twister, an excellent PRNG which distributes integers uniformly across the entire 32-bit range. Unfortunately, calling this PRNG 10000000 times does not tend to generate a sequence of 10000000 unique values. According to Hash Collision Probabilities, the probability of all 10000000 random numbers being unique is just:

That’s astronomically unlikely. In fact, the expected number of unique values in such sequences is only about 9988367. You can try it for yourself using Python:

>>> len(set([random.randint(0, 0xffffffff) for i in xrange(10000000)]))
9988432

One obvious refinement is to reject random numbers which are already in the sequence, and continue iterating until we’ve reached 10000000 elements. To check whether a specific value is already in the sequence, we could search linearly, or we could keep a sorted copy of the sequence and use a binary search. We could even track the presence of each value explicitly, using a giant 512 MB bitfield or a sparse bitfield such as a Judy1 array.

Another refinement: Instead of generating an arbitrary 32-bit integer for each element and hoping it’s unique, we could generate a random index in the range [0, N) where N is the number of remaining unused values. The index would tell us which free slot to take next. We could probably locate each free slot in logarithmic time by implementing a trie suited for this purpose.

Brainstorming some more, an approach based on the Fisher-Yates Shuffle is also quite tempting. Using this approach, we could begin with an array containing all possible 32-bit integers, and shuffle the first 10000000 values out of the array to obtain our sequence. That would require 16 GB of memory. The footprint could be reduced by representing the array as a sparse associative map, such a JudyL array, storing only those x where A[x] ≠ x. Or, instead of starting with an array of all possible 32-bit integers, we could start with an initial sequence of any 10000000 sorted integers. In an attempt to span the available range of 32-bit values, we could even model the initial sequence as a Poisson process.

All of the above approaches either run in non-linear time, or require large amounts of storage. Several of them would be workable for a sequence of just 10000000 integers, but it got me thinking whether a more efficient approach, which scales up to any sequence length, is possible.

A Non-Repeating Pseudo-Random Number Generator

The ideal PRNG for this problem is one which would generate a unique, random integer the first 2³² times we call it, then repeat the same sequence the next 2³² times it is called, ad infinitum. In other words, a repeating cycle of 2³² values. That way, we could begin the PRNG at any point in the cycle, always having the guarantee that the next 2³² values are repeat-free.

One way to implement such a PRNG is to define a one-to-one function on the integers – a function which maps each 32-bit integer to another, uniquely. Let’s call such a function a permutation. If we come up with a good permutation, all we need is to call it with increasing inputs { 0, 1, 2, 3, … }. We could even begin the input sequence at any value.

For some reason, I remembered from first-year Finite Mathematics that when p is a prime number, \(x^2\,\bmod\,p \) has some interesting properties. Numbers produced this way are called quadratic residues, and we can compute them in C using the expression x * x % p. In particular, the quadratic residue of x is unique as long as \(2x < p \). For example, when p = 11, the quadratic residues of 0, 1, 2, 3, 4, 5 are all unique:

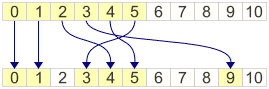
As luck would have it, it also happens that for the remaining integers, the expression p - x * x % p fits perfectly into the remaining slots. This only works for primes p which satisfy \(p \equiv 3\,\bmod\,4 \).

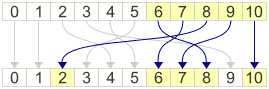
This gives us a one-to-one permutation on the integers less than p, where p can be any prime satisying \(p \equiv 3\,\bmod\,4 \). Seems like a nice tool for building our custom PRNG.

In the case of our custom PRNG, we want a permutation which works on the entire range of 32-bit integers. However, 2³² is not a prime number. The closest prime number less than 2³² is 4294967291, which happens to satisfy \(p \equiv 3\,\bmod\,4 \). As a compromise, we can write a C++ function which permutes all integers below this prime, and simply maps the 5 remaining integers to themselves.

unsigned int permuteQPR(unsigned int x)
{
    static const unsigned int prime = 4294967291;
    if (x >= prime)
        return x;  // The 5 integers out of range are mapped to themselves.
    unsigned int residue = ((unsigned long long) x * x) % prime;
    return (x <= prime / 2) ? residue : prime - residue;
}

This function, on its own, is not the world’s best permutation – it tends to cluster output values for certain ranges of input – but it is one-to-one. As such, we can combine it with other one-to-one functions, such as addition and XOR, to achieve a much better permutation. I found the following expression works reasonably well. The intermediateOffset variable acts as a seed, putting a variety of different sequences at our disposal.

permuteQPR((permuteQPR(x) + intermediateOffset) ^ 0x5bf03635);

On GitHub, I’ve posted a C++ class which implements a pseudo-random number generator based on this expression.

0xc2ab6929
0xa0e2502c
0x95b7c9eb
0x2fb14c01
0x5d983e09
0xba14e8c1
0x90994968
0x07058db1
0x061acc1f
0x969860fe
0x92f5a666
0xfa1b08af
0x18a3354f
...

I’ve also posted a working project to verify that this PRNG really does output a cycle of 2³² unique integers.

So, how does the randomness of this generator stack up? I’m not a PRNG expert, so I put my trust in TestU01, a library for testing the quality of PRNGs, published by the University of Montreal. Here’s some test code to put our newly conceived PRNG through its paces. It passes all 15 tests in TestU01’s SmallCrush test suite, which I guess is pretty decent. It also passes 140/144 tests in the more stringent Crush suite.

========= Summary results of SmallCrush =========

 Version:          TestU01 1.2.3
 Generator:        ursu_CreateRSU
 Number of statistics:  15
 Total CPU time:   00:00:49.95

 All tests were passed

Perhaps this approach for generating a sequence of unique random numbers is already known, or perhaps it shares attributes with existing PRNGs. If so, I’d be interested to find out. If you wanted, you could probably adapt it to work on ranges of integers other than 2³² as well. Surfing around, I noticed that OpenBSD implements another non-repeating PRNG, though I’m not sure their implementation is cyclical or covers the entire number space.

Incidentally, this PRNG is used in my next post, This Hash Table Is Faster Than a Judy Array.

Do you know any other way to solve this problem?