A hash function takes an item of a given type and generates an integer hash value within a given range. The input items can be anything: strings, compiled shader programs, files, even directories. The same input always generates the same hash value, and a good hash function tends to generate different hash values when given different inputs.

A hash function has no awareness of “other” items in the set of inputs. It just performs some arithmetic and/or bit-magic operations on the input item passed to it. Therefore, there’s always a chance that two different inputs will generate the same hash value.

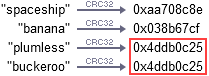
Take the well-known hash function CRC32, for example. If you feed this function the two strings “plumless” and “buckeroo”, it generates the same value. This is known as a hash collision.

What is the probability of a hash collision? This question is just a general form of the birthday problem from mathematics. The answer is not always intuitive, so it’s difficult to guess correctly. Let’s derive the math and try to get a better feel for those probabilities.

Calculating the Probability of a Hash Collision

There are many choices of hash function, and the creation of a good hash function is still an active area of research. Some hash functions are fast; others are slow. Some distribute hash values evenly across the available range; others don’t. If you’re interested in the real-world performance of a few known hash functions, Charles Bloom and strchr.com offer some comparisons. For our purposes, let’s assume the hash function is pretty good — it distributes hash values evenly across the available range.

In this case, generating hash values for a collection of inputs is a lot like generating a collection of random numbers. Our question, then, translates into the following:

Given \(k \) randomly generated values, where each value is a non-negative integer less than \(N \), what is the probability that at least two of them are equal?

It turns out it’s actually a bit simpler to start with the reverse question: What is the probability that they are all unique? Whatever the answer to the reverse question, we can just subtract it from one, and we’ll have the answer to our original question.

Given a space of \(N \) possible hash values, suppose you’ve already picked a single value. After that, there are \(N-1 \) remaining values (out of a possible \(N \)) that are unique from the first. Therefore, the probability of randomly generating two integers that are unique from each other is \(\frac{N-1}{N} \).

After that, there are \(N-2 \) remaining values (out of a possible \(N \)) that are unique from the first two, which means that the probability of randomly generating three integers that are all unique is \(\frac{N-1}{N}\times\frac{N-2}{N} \). (We can multiply the probabilities together because each random number generation is an independent event.)

In general, the probability of randomly generating \(k \) integers that are all unique is:

On a computer, this can be quite slow to evaluate for large k. Luckily, the above expression is approximately equal to:

which is a lot faster to compute. How do we know this is a good approximation? Well, it can be shown analytically, using the Taylor expansion of \(e^x \) and an epsilon-delta proof, that the approximation error tends to zero as \(N \) increases. Or, you can just compute both values and compare them. Run the following Python script with different \(N \), and you’ll get a feeling for just how accurate the approximation is:

import math
N = 1000000
probUnique = 1.0
for k in xrange(1, 2000):
    probUnique = probUnique * (N - (k - 1)) / N
    print k, 1 - probUnique, 1 - math.exp(-0.5 * k * (k - 1) / N)

Great, so this magic expression serves as our probability that all values are unique. Subtract it from one, and you have the probability of a hash collision:

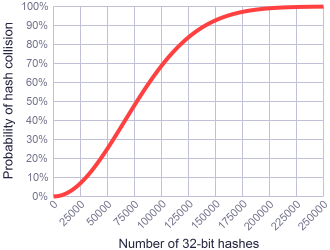
Here is a graph for \(N = 2^{32} \). This illustrates the probability of collision when using 32-bit hash values. It’s worth noting that a 50% chance of collision occurs when the number of hashes is 77163. Also note that the graph takes the same S-curved shape for any value of \(N \).

Simplified Approximations

It’s interesting that our approximation takes the form \(1 - e^{-X} \), because it just so happens that for any \(X \) that is very small, say \(\frac{1}{10} \) or less:

In other words, the exponent makes a pretty good approximation all by itself! In fact, the smaller the \(X \), the more accurate it gets. So for small collision probabilities, we can use the simplified expression:

This is actually a handy representation, because it avoids some numerical precision problems in the original expression. Floating point numbers are not very good at representing values extremely close to 1.

Furthermore, if you’re talking about more than a handful of \(k \), there isn’t a very big difference between \(k(k-1) \) and \(k^2 \). So the absolute simplest approximation is just:

Small Collision Probabilities

In certain applications — such as when using hash values as IDs — it can be very important to avoid collisions. That’s why the most interesting probabilities are the small ones.

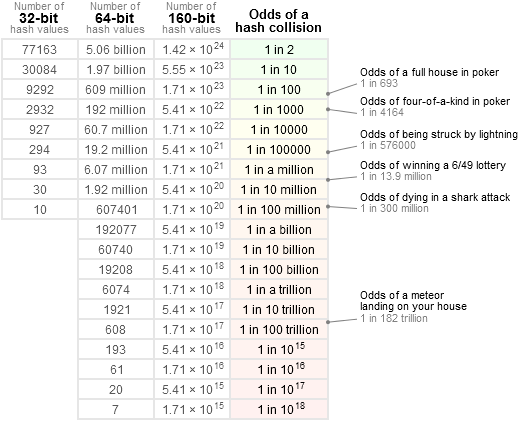
Assuming your hash values are 32-bit, 64-bit or 160-bit, the following table contains a range of small probabilities. If you know the number of hash values, simply find the nearest matching row. To help put the numbers in perspective, I’ve included a few real-world probabilities scraped from the web, like the odds of winning the lottery.