In game development, we use associative maps for many things. Dynamic loading, object reflection, rendering, shader management.

A lot of them fit the following usage pattern:

• The keys and values have simple integer or pointer types.
• The keys are effectively random.
• The basic operation is lookup-or-insert: Look for an existing item first, and add one if not found. Usually, the item is found.
• Deletes happen infrequently, and when they do, they tend to happen in bulk.

Occasionally, one of these maps is identified as a performance bottleneck. It raises the question: What’s the best data structure to use in this scenario?

I wrote a small C++ application to compare two top candidates, a Judy array and a finely-tuned hash table, using various experiments. All the code is available on GitHub.

A Judy array – specifically, the JudyL variant – is an efficient mapping of integer keys to integer values. It is optimized to avoid CPU cache misses as often as possible. Its memory consumption scales smoothly with number of entries, even when the keys are sparsely distributed. It’s a real feat of engineering – hats off to Doug Baskins.

A hash table is a relatively well-known data structure. For this post, I’ve written a custom hash table based on open addressing with linear probing. This particular hash table will dynamically resize itself as the population grows.

Now, there are already several existing shootouts between Judy arrays and hash tables on the web. Some of them are good, but in this post, I wanted to target a very specific usage pattern. Also, I wrote the single most efficient integer hash table I could, with the explicit goal of taking Judy down – no smorgasbord of lame hash tables here. Finally, I took considerable pains to ensure that the benchmarking method produced fair, precise and detailed results, as outlined in the README. Feedback is welcome.

Adding Items to the Map

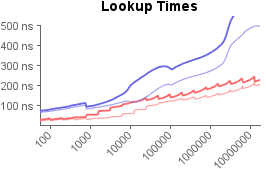
In this experiment, more than 10000000 unique 32-bit random keys are inserted into each map, and the insertion times are measured. The timings were taken on my aging Core 2 Duo E6300.

Each point on the graph represents the time to insert the Nth element into a map containing N - 1 elements, averaged around small neighborhoods of N.

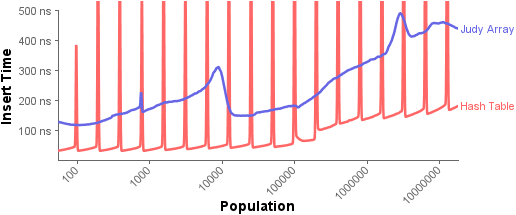
First, you’ll notice all the spikes in the hash table insertion times. These spikes are due to dynamic resizing of the hash table, which comes at a cost. Once the table becomes 75% full – for example, when the 12280th item is inserted into a hash table of size 16384 – we dynamically allocate a new hash table with double the size, copy all existing items to new hash slots, and delete the old table. As you’d expect, this operation is slow. For example, where most items take between 30 and 40 nanoseconds to insert, the 12280th item takes 0.4 milliseconds.

That’s expensive, but remember, resizing happens infrequently. In practice, these one-time costs are amortized against thousands of other insert operations that run very quickly. Another way to look at it is that the area under the red curve is much smaller than the area under the blue curve, meaning that the total CPU time spent inserting into the hash table is much less, even with the presence of spikes. And in cases where it really matters, you could always pre-allocate the hash table to a large enough size, eliminating those spikes completely.

Judy makes heavy use of the memory allocator, so to show it in its best light, I hardwired the Judy array to DLMalloc. DLMalloc is a great allocator, and helps avoid the possibility of hidden performance pitfalls on Windows, such as DLL runtime overhead and (God forbid) the debug system heap.

It should be acknowledged that Judy insertion times are faster in cases when the keys are not random; however, that’s not what we’re testing in this experiment.

Finding Existing Items in the Map

Usually, during the lookup-or-insert operation, an existing item is already found in the map. That makes lookup times even more significant than insert times.

In this next experiment, each map is filled to various populations. At each population, thousands of random lookups are performed, and the average time per lookup is plotted. Here, the lookup function is actually the same as the insert function used in the previous experiment – the only difference is that this time, we call it using keys that are known to already exist in the map.

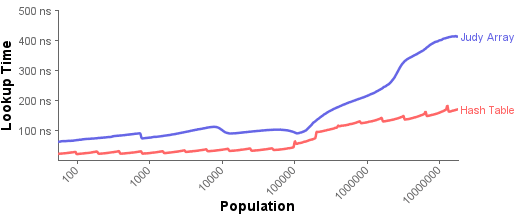
At all populations, hash table lookups are twice as fast as Judy array lookups, give or take. I suspect part of the reason is because hash tables cause even fewer cache misses than Judy. With a good hash function, most lookups should be found in the first memory address checked; if not, linear probing ensures they are likely to be found in the same cache line. Notice that when the population reaches 98304 items, the hash table stops fitting entirely within the CPU’s 2 MB L2 cache, which is when the lookup times begin to climb.

Because the keys are random, the choice of hash function doesn’t matter too much for this experiment. Nonetheless, I borrowed MurmurHash3’s integer finalizer as the hash function. It consists of a few XORs, multiplies and shifts, and seems to distribute the hashes just as effectively when the keys are not random.

h ^= h >> 16;
h *= 0x85ebca6b;
h ^= h >> 13;
h *= 0xc2b2ae35;
h ^= h >> 16;

I chose not to benchmark the delete operation, because under the given usage pattern, deletes tend to be one-time operations that happen in bulk, such as when unloading a section of a game world. Still, one cool thing about hash tables with linear probing is that the Delete method needs only to shuffle existing entries around. This hash table also offers a Compact method, to optionally reclaim memory. Finally, you could write an even faster delete function if you require that Compact is always called at the end of each bulk delete.

Polluting the CPU Cache Between Operations

The above experiments are purely micro-benchmarks, which makes them somewhat unrealistic. A real application would run plenty of other code in between operations on the map. This would continuously evict parts of the map from the CPU cache, which would have a direct impact on the map’s performance.

With that in mind, I added some artificial cache pollution to both experiments, and ran them again. This time, random chunks of memory were manipulated between each operation. Using this strategy, I collected two extra datasets for each data structure, and plotted them below. The thin lines have an average of 1000 bytes of cache pollution between operations, while the thick lines have an average of 10000 bytes.

 

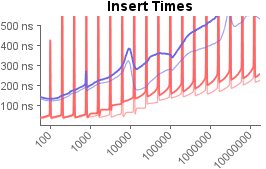
As you can see, cache pollution makes all of the timings slower, especially at larger populations. Regardless, the hash table still runs roughly twice as fast as the Judy array at nearly all populations and pollution levels.

Obviously, the most useful performance measurements would be taken in a real application using a consistently reproducible test case. For such measurements, an APIProfiler-like profiling technique comes in handy.

Memory Consumption

Judy is known for its memory-efficiency. So, how does its memory consumption compare to that of the hash table? To find the answer, I called dlmalloc_stats, a function that includes the overhead of the memory allocations themselves, an intrinsic cost that is all-too-easily overlooked. This graph plots the total bytes consumed by each map, divided by the total number of items in the map.

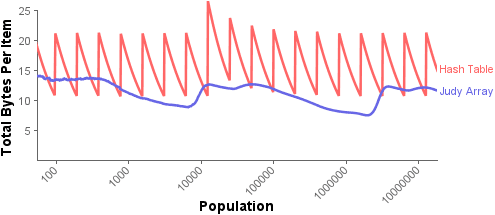
You can see that the hash table’s memory consumption follows a sawtooth pattern, doubling in size each time the 75% threshold is reached. Judy’s memory consumption, on the other hand, scales much more smoothly, and tends to hover around the lower end of the hash table’s amount. Still, there are some points where the two lines cross, which means that the hash table actually takes less memory at certain populations. Beyond 1000 items, though, those cases are generally the exception.

Judy also has the interesting ability to consume even less memory when the keys are not distributed randomly. In particular, when all the keys are clustered around a small range, its memory consumption tends towards that of a plain array. That’s impressive, but again, not the usage pattern we’re testing in this experiment.

Conclusion

For the given usage pattern, a Judy array is not the fastest associative map. But for general use, Judy arrays tend to be among the fastest associative maps while also being among the most memory-efficient, which is what made them a contender here in the first place. As a bonus, Judy arrays are always sorted. That means you can iterate sequentially through the map at any moment, something not possible using a hash table – though this property generally does not bring any benefit in the usage pattern studied here. Judy is also LGPL-licensed and patented, which may make it unsuitable for certain kinds of development.

The hash table tested here was specifically written for the job. In general, you can’t just grab any module with “hash table” in the name, slap it in place and expect the same performance. The addressing strategy, choice of hash function, handling of free/deleted slots, and reliance on inlining, templates and indirection each has the potential to bog down the CPU in various ways.

Another fun, useful fact about this type of hash table is that it lends itself surprisingly well to lock-free programming. You can read all about it in my follow-up post, The World’s Simplest Lock-Free Hash Table.