In my previous post, I shared some source code to sort one million 8-digit numbers in 1MB of RAM as an answer to this Stack Overflow question. The program works, but I didn’t explain how, leaving it as a kind of puzzle for the reader.

I had promised to explain it in a followup post, and in the meantime, there’s been a flurry of discussion in the comments and on Reddit. In particular, commenter Ben Wilhelm (aka ZorbaTHut) already managed to explain most of it (Nice work!), and by now, I think quite a few people already get it. Nonetheless, I’ll write up another explanation as promised.

Data Structures

In this implementation, there is a staging area and a circular buffer. The staging area is just big enough to hold 8000 plain 32-bit integers. The circular buffer always holds a sorted sequence of numbers, using a compact representation which we’ll get to shortly.

We read numbers into the staging area until it’s full. Once it’s full, we sort it in-place, then merge it with the sorted contents of the circular buffer. The merge is basically the same merge operation performed in Mergesort, but we conserve memory using a trick: The new sequence is written to the buffer immediately following the previous one, and the previous sequence is erased while it’s read. This being a circular buffer, we wrap around to the beginning of the buffer once we’ve reached the end.

These steps are repeated until all of the input is read and the final staging area is merged. At that point, we have the entire sorted sequence stored in our circular buffer.

The staging area is really just an optimization. Theoretically, we don’t need it – we could merge each input number directly into the circular buffer as it comes in. The only problem is that as the sorted sequence grows, the merge operation becomes very slow, mainly due to the decoding and re-encoding process that’s involved. In fact, if you increase the staging area to hold 20000 integers instead of just 8000, the program runs twice as fast. That’s why I made the staging area as large as possible in the available memory.

A Sequence of Deltas

Next, we need a way to fit the sorted number sequence into a circular buffer significantly less than 1MB (1048576 bytes) in size. Many people on Stack Overflow and Reddit came up with this idea, which is indeed where I got it: Instead of storing the actual numbers, we store a delta sequence – the differences from one number to the next. Because the sequence is already sorted, these delta values tend to be quite small. In fact, given a sequence of N 8-digit numbers, the average delta value is just

$$\frac{100000000}{N}$$

By the time we’ve reached a million numbers, the average delta shrinks to just 100. Deltas around this size can be represented using 7 bits, since 2⁷ = 128, so intuitively, you can begin to see the potential to save memory. It’s also OK to use a lot more bits to represent larger delta values, since those appear far less frequently. The bigger the delta, the sooner we start to reach the end of the list!

Encoding Each Delta

All that’s left to explain is how we actually encode each delta value. Since each one will use a variable number of bits, it helps to look at the circular buffer as a bit stream, which is what BitReader and BitWriter are for.

There are many ways to encode them, and it’s tough to find a strategy which respects our extremely limited memory budget in every case. For example, this comment describes an encoding strategy which takes 1000000 bytes in the case where every delta is less than 128, but up to 1564452 bytes when other delta values are mixed in.

It turns out that the optimal encoding strategy is arithmetic coding. But before jumping into that, let’s first take a look at an alternate encoding strategy which requires a bit more memory than we’re allowed, but is much easier to understand. This alternate coding also has a few similarities to the arithmetic coding implementation I wrote, so it’ll serve as a pretty good warm-up to that one.

In this alternate strategy, we decode the next delta value as follows. Define an integer variable accumulator, initialize it to 0, then look at the incoming bit stream:

• If the next bit is 1, add 64 to accumulator and repeat.
• If the next bit is 0, read a 6-bit integer from the bitstream, add it to accumulator and return accumulator as the delta.

How much memory does this strategy need to represent an entire number sequence? Well, each delta value will require at least one 0 followed by 6 bits, and we’re going to have a million of those. On top of that, each leading 1 causes our sequence value to increase by 64, which obviously can’t happen more than \(\frac{100000000}{64} \) times. Using this strategy, every possible sequence should fit within

$$7 \times 1000000 + \displaystyle\frac{100000000}{64} = 8562500 \text{ bits} \approx {\bf 1070312.5} \text{bytes}$$

Indeed, a sequence where all deltas are zero except for one 99999999 requires exactly that many bits. That’s more than 21KB over budget, so we have to do better.

Effectively, the above strategy follows a path determined by the bit stream to arrive at the next delta value. Here’s a graph to illustrate several possible bit paths:

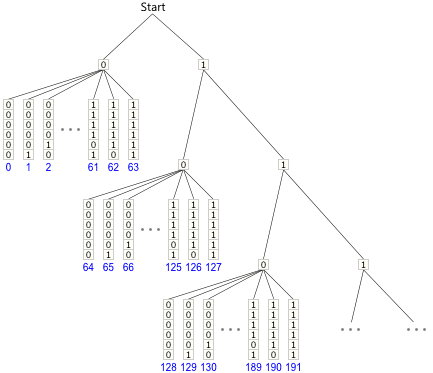
For those who don’t already recognize it, this turns out to be a Huffman encoding tree. Huffman coding is really just a special case of arithmetic coding. (And as commenter Stergios Stergiou points out, this particular style of Huffman coding is known as Golomb coding.)

When arithmetic coding is used, the entire sequence fits safely within < 1013000 bytes, all the time. This strategy proved kind of challenging to implement, so it took the most time to get right. In the next two posts, I’ll describe how it was implemented using all that fancy bit magic you see in Decoder::decode and Encoder::encode.